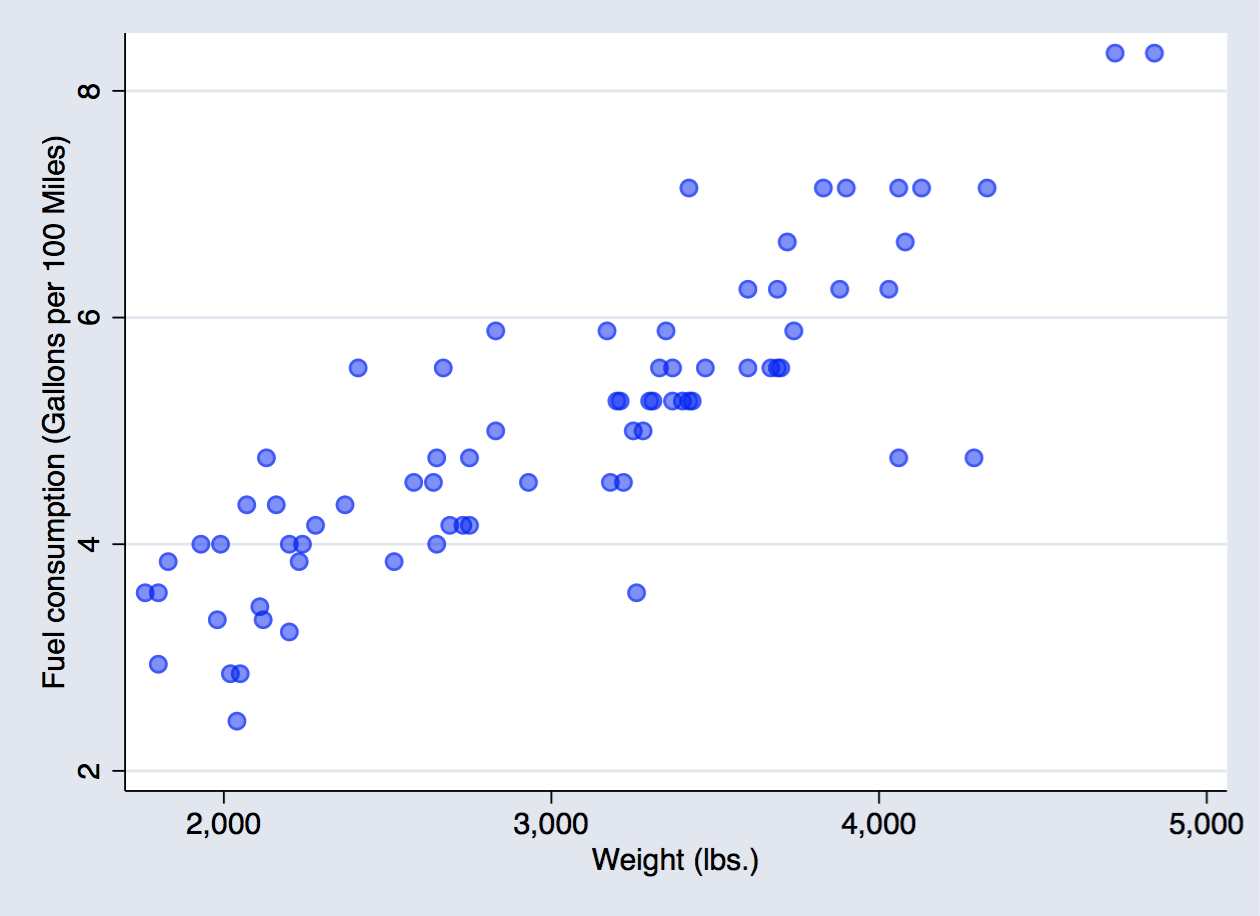
scatter fuel weight
We conduct a study of the fuel consumption of cars in Stata's auto dataset.
. sysuse auto, clear
(1978 Automobile Data)
We generate a variable, fuel, that measures the fuel consumption rate in the unit of Gallons per 100 Miles.
. generate fuel = 100/mpg
. label variable fuel "Fuel consumption (Gallons per 100 Miles)"
We examine variables for possible errors in the data.
. describe fuel weight
storage display value
variable name type format label variable label
--------------------------------------------------------------------------------
fuel float %9.0g Fuel consumption (Gallons per 100
Miles)
weight int %8.0gc Weight (lbs.)
. summarize weight
Variable | Obs Mean Std. Dev. Min Max
-------------+---------------------------------------------------------
weight | 74 3019.459 777.1936 1760 4840
The variable weight has minimum value 1760.00, maximum value 4840.00, and range 3080.00.
. scatter fuel weight, mcolor(blue%50)

scatter fuel weight
. regress fuel weight
Source | SS df MS Number of obs = 74
-------------+---------------------------------- F(1, 72) = 194.71
Model | 87.2964969 1 87.2964969 Prob > F = 0.0000
Residual | 32.2797639 72 .448330054 R-squared = 0.7300
-------------+---------------------------------- Adj R-squared = 0.7263
Total | 119.576261 73 1.63803097 Root MSE = .66957
------------------------------------------------------------------------------
fuel | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
weight | .001407 .0001008 13.95 0.000 .001206 .0016081
_cons | .7707669 .3142571 2.45 0.017 .1443069 1.397227
------------------------------------------------------------------------------
The regression shows that for every unit increase in weight, a 0.0014 unit increase in fuel consumption is predicted.